Josef Troch (troch@mail.ru)
14.4.2002
Slévání v konstantním prostoru (a v lineárním čase)
(Linear time merging in constant extra space)
Úloha:
Máme dáno pole (délky n) sestávající ze 2 setříděných neklesajících posloupností
(obecně různě dlouhých):
R1 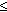 ...
... 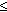 Rk a
Rk+1
Rk a
Rk+1 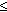 ...
... 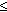 Rn
Rn
Naším úkolem je ukázat algoritmus, který slije tyto dvě posloupnosti do jedné - tj. vytvoří z nich
jednu setříděnou posloupnost; při čemž požadujeme, aby algoritmus pracoval v čase O(n) a
používal pomocnou paměť o velikosti pouze O(1).
Tato úloha bývá označována také jako slévání "na místě" v lineárním čase (linear time in
situ merging).
Pozn.: Prvky pole číslujeme od 1, nikoliv od 0. Dále nebudeme pro jednoduchost rozlišovat mezi prvkem a
hodnotou jeho klíče - tedy budeme předpokládat, že klíčem je celý prvek.
Nevyhovující řešení:
Klasické metody pro slévání (viz např. [Knuth]) sice pracují v lineárním čase, ale
používají pomocnou paměť o velikosti O(n).
Opačně, metodou, která dá požadovaný výsledek a pracuje "na místě" (tedy s pomocnou pamětí
velikosti O(1)), je heapsort (opět viz např. [Knuth])- ten ovšem potřebuje čas O(n.log(n)).
Jednodušší algoritmus (M. A. Kronrod):
První algoritmus řešící danou úlohu byl publikován Michailem Aleksandrovičem Kronrodem
[Kronrod] v r. 1969. Ačkoliv se může zdát složitým, patří k nejjednodušším algoritmům
řešícím daný problém. Bohužel jsem neměl k dispozici původní Kronrodovu práci, takže jsem musel vycházet z
velmi stručného shrnutí algoritmu v knize [Knuth].
- Buď s=
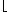
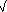 n
n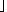 . Rozdělíme pole (obsahující zmíněné
posloupnosti) na bloky délky s, poslední blok (necelý) bude mít délku n mod s
(což může být 0). Označme počet celých bloků m + 1, bloky označme
B1 ... Bm, Bm+1, Bm+2 (kde
Bm+2 je ten necelý popř. prázdný blok).
. Rozdělíme pole (obsahující zmíněné
posloupnosti) na bloky délky s, poslední blok (necelý) bude mít délku n mod s
(což může být 0). Označme počet celých bloků m + 1, bloky označme
B1 ... Bm, Bm+1, Bm+2 (kde
Bm+2 je ten necelý popř. prázdný blok).
- Nyní vyměníme prvky v bloku Bm+1 s blokem obsahujícím prvek Rk.
Pole tedy nyní má tuto strukturu:
B1 ... Bm , A
- kde každý z bloků B1 ... Bm má právě s prvků, setříděných
do neklesající posloupnosti a A je pomocná (auxiliary) oblast obsahující t prvků,
pro nějaké t, kde s 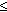 t < 2s . (A obsahuje právě prvky z bloku, který
obsahoval Rk a z bloku Bm+2 .}
t < 2s . (A obsahuje právě prvky z bloku, který
obsahoval Rk a z bloku Bm+2 .}
- Najdeme blok s nejmenším prvním (=nejlevějším) prvkem (porovnáváme tedy prvky v poli na pozicích 1,
s + 1, ..... (m - 1).s + 1) a vyměníme tento blok s blokem
B1 . Pak najdeme blok s druhým nejmenším nejlevějším prvkem a vyměníme ho s
B2 atd. Bloky jsou tedy nyní uspořádány tak, že jejich nejlevější prvky tvoří
neklesající posloupnost. Zároveň platí, že počet inverzí (viz níže) libovolného
prvku v oblasti B1 ... Bm je menší než s
(viz níže).
- Nyní slijeme blok B1 s blokem B2 následujícím způsobem: Vyměníme
B1 s prvními s prvky v A (označme tuto oblast A'). Pak sléváme
blok B2 s prvky z oblasti A' (tedy s bývalým obsahem bloku B1)
do oblasti B1B2 tak, že vyměňujeme prvky B1B2 s
těmi, které přichází na jejich místo coby slitá posloupnost (viz př. č. 2).
Tímto zrušíme uspořádání prvků v oblasti A'.
Stejným způsobem poté slijeme B2 s B3, pak B3 s
B4, .... Bm-1 s Bm. Nyní máme setříděnu celou
oblast B1 ... Bm (viz níže).
- Setřídíme oblast prvků Rn-2t+1 ... Rn (tedy 2t posledních prvků
v poli - bez ohledu na hranice bloků) pomocí třídění přímým výběrem (straight selection sort - viz
[Knuth]). (Obecně lze použít libovolnou metodu pracující na místě v čase
O((2t)2)=0(n) .) Tímto dostaneme t největších prvků do oblasti A.
- Slijeme oblasti Rn-2t+1 ... Rn-t a R1 ...
Rn-2t s použitím pomocné oblasti A (obdobně jako dříve). Nyní máme opět setříděnu celou
oblast B1 ... Bm, avšak oblast A již obsahuje t největších
prvků.
- Setřídíme oblast A přímým výběrem. Nyní máme setříděné již celé pole.
Příklad
Př. č. 1.:
Mějme na vstupu tyto dvě posloupnosti (n=21, k=11):
01 04 04 05 06 08 09 10 11 14 19 | 02 03 04 06 07 10 14 16 17 18
Po 1. kroku algoritmu: 01 04 04 05 06 | 08 09 10 11 14 | 19 02 03 04 06 | 07 10 14 16 17 | 18
Po 2. kroku algoritmu: 01 04 04 05 06 | 08 09 10 11 14 | 07 10 14 16 17 | 19 02 03 04 06 | 18
Po 3. kroku algoritmu: 01 04 04 05 06 | 07 10 14 16 17 | 08 09 10 11 14 | 19 02 03 04 06 | 18
Pro další kroky algoritmu je již příklad zbytečný, s vyjímkou kroku 4., který si zaslouží
podrobnější rozepsání.
Př. č. 2.:
Rozebereme první fázi kroku 4 (tedy slití B1 a B2). Buď
s = 3 a x1 < y1 < x2 < y2 < x3 < y3.
| |
B1 |
B1 |
A' |
| Iniciální stav |
x1 x2 x3 |
y1 y2 y3 |
a1 a2 a3 |
| Výměna B1 a A' |
a1 a2 a3 |
y1 y2 y3 |
x1 x2 x3 |
| x1 do slité posloupnosti |
x1 a2 a3 |
y1 y2 y3 |
a1 x2 x3 |
| y1 do slité posloupnosti |
x1 y1 a3 |
a2 y2 y3 |
a1 x2 x3 |
| x2 do slité posloupnosti |
x1 y1 x2 |
a2 y2 y3 |
a1 a3 x3 |
| y2 do slité posloupnosti |
x1 y1 x2 |
y2 a2 y3 |
a1 a3 x3 |
| x3 do slité posloupnosti |
x1 y1 x2 |
y2 x3 y3 |
a1 a3 a2 |
(Slévání můžeme ukončit okamžitě po té, co byl vyměněn s-tý prvek oblasti A'.)
Proč algoritmus funguje:
Většina potřebných informací byla uvedena již v samotném algoritmu, zde uvádím důkazy jediných dvou v
algoritmu uvedených tvrzení, která nejsou zcela zřejmá.
- Definujme počet inverzí prvku Ri jako počet prvků
Rj takových, že Rj > Ri a zároveň j < i.
(Tedy počet prvků, které jsou větší než Ri, ale jsou před ním v poli.)
- Tvrzení 1.1: Po 3. kroku algoritmu platí, že počet inverzí
libovolného prvku (označme ho Ri) z oblasti
B1 ... Bm je menší než s.
Důkaz: Označme blok obsahující Ri jako Bx. Uvažujme blok
By nacházející se v oblasti před Ri.
-
Tento blok může pocházet ze stejné vstupní posloupnosti jako Ri , v tomto případě ale
Bx a By jsou 2 celistvé úseky jedné ze vstupních posloupností a
nejlevější prvek By je
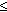 nejlevější prvek bloku Bx ,
a proto všechny prvky v By jsou
nejlevější prvek bloku Bx ,
a proto všechny prvky v By jsou 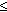 než Ri. Tento blok nám tedy
nezvýší počet inverzí.
než Ri. Tento blok nám tedy
nezvýší počet inverzí.
-
Pokud ovšem By náležel do druhé vstupní posloupnosti než Ri , můžeme
rozlišit 2 případy. Buď je nejpravější prvek (a tedy i všechny ostatní prvky) By
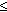 Ri - počet inverzí se nám nezvýší; nebo je nejpravější prvek By
větší než Ri - ovšem nejlevější prvek By je určitě
Ri - počet inverzí se nám nezvýší; nebo je nejpravější prvek By
větší než Ri - ovšem nejlevější prvek By je určitě 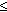 nejlevější prvek bloku Bx a tudíž By nám zvýší počet
inverzí maximálně o s - 1 . Nicméně takovýto blok se může před Ri
vyskytnout pouze jeden - pokud by někde za By následoval druhý blok ze stejné
posloupnosti, jeho nejlevější prvek by musel být větší nebo roven nejpravějšímu prvku
By , ovšem tím by byl větší než Ri a tedy i větší než
nejlevější prvek Bx, tedy by následoval v poli až za Ri.
nejlevější prvek bloku Bx a tudíž By nám zvýší počet
inverzí maximálně o s - 1 . Nicméně takovýto blok se může před Ri
vyskytnout pouze jeden - pokud by někde za By následoval druhý blok ze stejné
posloupnosti, jeho nejlevější prvek by musel být větší nebo roven nejpravějšímu prvku
By , ovšem tím by byl větší než Ri a tedy i větší než
nejlevější prvek Bx, tedy by následoval v poli až za Ri.
- Tvrzení 1.2: Po 4. kroku algoritmu je setříděna již celá oblast
B1 ... Bm .
Důkaz: Ukážeme, že počet inverzí libovolného prvku z dané oblasti je po 4. kroku algoritmu 0, a
tedy je posloupnost setříděná (protože před žádným prvkem Ri není prvek větší než
Ri).
Pro libovolný prvek Ri z dané oblasti před tímto krokem platilo, že jeho počet inverzí
je menší než s. Označme blok obsahující Ri jako Bx ,
předpokládejme, že x ≠ 1 (při x = 1 je počet inverzí
Ri již před tímto krokem roven 0). V okamžiku, kdy sléváme blok Bx s
blokem Bx-1, Bx-1 obsahuje s největších prvků ležících před
Ri a tedy po slití těchto dvou bloků klesne počet inverzí prvku Ri
na 0 (a blok Bx bude opět obsahovat s největších prvků z oblasti
B1 ... Bx).
Časová složitost:
Rozebereme jednotlivé kroky:
- V tomto kroku se jen vypočítají s a m, což lze v čase O(1).
- Výměna dvou bloků zabere triviálně čas O(s).
- Nalezení bloku s nejmenším nejlevějším prvkem zabere O(m), výměna dvou bloků O(s). Toto
opakujeme m - 1 krát, tedy celkový čas je O(m .(m + s)).
- Slití dvou bloků zabere čas O(s), tedy celý tento krok O(m . s).
- Třídění přímým výběrem - O((2t)2).
- Slití těchto 2 posloupností potřebuje čas O(n).
- Třídění přímým výběrem - O(t2).
Sečteme-li tedy časové složitosti jednotlivých kroků (s použitím výše uvedených definic s, m, t),
zjistíme, že algoritmus běží v požadovaném čase O(n).
Poznámky k algoritmu:
- Algoritmus není stabilní (stable) - tedy nezachovává pořadí stejně velkých prvků. Toto lze
postřehnout z př. č. 2, kde se v závislosti na obsazích slévaných bloků permutují
prvky v pomocné oblasti A'.
- Algoritmus zjevně není příliš efektivní.
- [Knuth] všude používá místo třídění přímým výběrem insertsort, tedy třídění
vkládáním.
Rychlejší algoritmus (B. C. Huang & M. A. Langston):
Kronrodův algoritmus pracuje sice v čase O(n) = c . n, ale konstanta c je u
něj poměrně vysoká. Bin-Chao Huang a Michael A. Langston v roce 1988 navrhli algoritmus, který řeší
tentýž problém (a zjevně vychází z Kronrodova algoritmu), ale je o poznání rychlejší, tedy i použitelnější v
praxi (měl by být méně než dvakrát pomalejší než rychlá implementace klasického slévání). Jak by se dalo
předpokládat, algoritmus je o něco složitější. Tato část článku byla zpracována podle původní práce autorů
[Huang, Langston].
Zjednodušená varianta algoritmu:
Pro jednoduchost nyní předpokládejme, že n je druhá mocnina nějakého přirozeného čísla
s a že jsme schopni přemístit s největších prvků pole na jeho počátek (jejich pořadí zde je
nepodstatné) tak, že za nimi následují zbylé části vstupních posloupností a že počet prvků v každé z nich (po
výše uvedeném odebrání nejvyšších prvků) je nějakým celým násobkem čísla s. Jak upravit vstup, aby
splňoval tyto požadavky je uvedeno níže.
Pro snadnější pochopení algoritmu doporučuji si v průběhu jeho studia prohlédnout níže uvedený
příklad.
- Spočteme s a rozdělíme pole na bloky délky s. Bloky označme
B1 ... Bs . Nejlevější prvek bloku Bi označme
head(Bi ), nejpravější tail(Bi ).
Použijeme algoritmus z předpokladů, čímž přesuneme s největších prvků pole na jeho počátek.
- Setřídíme bloky B2 ... Bs podle jejich nejpravějších prvků
(tail(Bi )) - obdobně jako v 3. kroku Kronrodova
algoritmu).
- Nyní vybereme 2 "běhy", které budeme slévat. Prvním běh budou bloky
B2 ... Bi (i
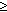 2), kde Bi
je první blok takový, že tail(Bi ) > head(Bi+1 ).
Druhý běh bude sestávat pouze z bloku Bi+1.
2), kde Bi
je první blok takový, že tail(Bi ) > head(Bi+1 ).
Druhý běh bude sestávat pouze z bloku Bi+1.
- Pomocnou (auxiliary) oblastí (tu zde chápeme jako sadu prvků, ne sadu pozic jako v Kronrodově
algoritmu!) je momentálně blok B1. Sléváme první a druhý běh tak, že vždy porovnáme
nejlevější nepřesunutý prvek v 1. běhu s nejlevějším nepřesunutým prvkem v 2. běhu a ten menší z nich
(jsou-li stejné, bereme ten levý) vyměníme s nejlevějším prvkem pomocné oblasti. Pomocná oblast se nám
tedy v průběhu slévání typicky rozdělí na 2 části (a její prvky se v poli postupně přesouvají doprava).
Slévání ukončíme v okamžiku, kdy tail(Bi ) je přesunut na svou finální pozici.
V tomto okamžiku je rovněž pomocná oblast jedním souvislým úsekem, ačkoliv nemusí začínat na hranici
bloku. Z bloku Bi+1 nám musel zůstat 1 či více nepřesunutých prvků (protože bloky
byly setříděny dle svých tail(...) - tedy
tail(Bi ) 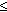 tail(Bi+1 ) a v případě stejných prvků
jsme vzali ten levý).
tail(Bi+1 ) a v případě stejných prvků
jsme vzali ten levý).
- Vybereme nové 2 běhy - první běh bude začínat nejlevějším nepřesunutým prvkem z
Bi+1 a končit (analogicky ke kroku 3.) prvkem tail(Bj )
(j
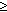 i+1), kde Bj je první blok (popř. ten nepřesunutý zbytek bloku
Bi+1) takový, že
tail(Bj ) > head(Bj+1 ). Druhý běh bude odpovídat
bloku Bj+1. Tyto běhy výše uvedeným způsobem slijeme (s použitím té pomocné oblasti,
která se nám posunula doprava). Pokračujeme tedy cyklicky v hledání běhů a jejich slévání, do okamžiku,
kdy se nám podaří nalézt již jen jediný běh.
i+1), kde Bj je první blok (popř. ten nepřesunutý zbytek bloku
Bi+1) takový, že
tail(Bj ) > head(Bj+1 ). Druhý běh bude odpovídat
bloku Bj+1. Tyto běhy výše uvedeným způsobem slijeme (s použitím té pomocné oblasti,
která se nám posunula doprava). Pokračujeme tedy cyklicky v hledání běhů a jejich slévání, do okamžiku,
kdy se nám podaří nalézt již jen jediný běh.
- Tento běh tedy posuneme doleva ("rotace") tak, že se nám pomocná oblast dostane na pravý konec
pole (jak toto provést efektivně viz níže).
- Na závěr setřídíme pomocnou oblast přímým výběrem. Máme setříděno celé pole.
Tento příklad byl převzat z [Huang, Langston].
Velkými písmeny jsou znázorněny jednotlivé prvky (záznamy), prvky (klíče prvků) se stejnými písmeny mají
stejnou hodnotu. Indexy udávají, o který prvek (z těch se stejnou hodnotou) jde - z toho lze postřehnout,
že metoda není stabilní.



Proč algoritmus funguje:
- Definujme počet opačných inverzí prvku Ri jako počet
prvků Rj takových, že Rj < Ri a zároveň
j > i. (Tedy zcela obráceně k definici inverze v Kronrodově
algoritmu - počet prvků, které jsou menší než Ri, ale jsou za ním v poli.)
- Tvrzení 2.1: Po provedení 2. kroku je počet opačných inverzí libovolného prvku v
oblasti B2 ... Bs menší než s, všechny tyto inverze
pocházejí ze stejného bloku.
Důkaz: (Dokazované tvrzení je "převráceným" tvrzením k 1.
tvrzení u Kronrodova algoritmu, důkaz je také principielně stejný, proto jen stručně.)
Zvolme libovolný prvek Ri neležící v pomocné oblasti. Označme blok, který ho
obsahuje Bx. Uvažujme blok By nacházející se v oblasti za
Ri.
- Tento blok může pocházet ze stejné vstupní posloupnosti jako Ri , v tomto
případě jsou všechny jeho prvky větší nebo rovny Ri, neboť bloky jsou setříděny
dle nejpravějších prvků. Počet opačných inverzí se nám nezvýší.
- Pokud By náležel do druhé vstupní posloupnosti než Ri,
můžeme rozlišit 2 případy. Buď je head(By ) (a tedy i všechny ostatní
prvky By ) větší nebo roven Ri - počet opačných
inverzí se nám nezvýší; nebo je head(By ) < Ri -
ovšem
tail(By )
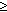 tail(Bx )
tail(Bx ) 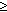 Ri
a tudíž By nám zvýší počet opačných inverzí maximálně o
s - 1 . Ale takovýto blok se může za Ri vyskytnout pouze
jeden - pokud by někde za By následoval druhý blok ze stejné posloupnosti,
všechny jeho prvky by byly
Ri
a tudíž By nám zvýší počet opačných inverzí maximálně o
s - 1 . Ale takovýto blok se může za Ri vyskytnout pouze
jeden - pokud by někde za By následoval druhý blok ze stejné posloupnosti,
všechny jeho prvky by byly
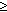 tail(By )
tail(By ) 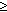 Ri.
Ri.
- Tvrzení 2.2: Po provedení 5. kroku algoritmu je část pole vlevo od pomocné oblasti
setříděna, libovolný prvek vpravo od pomocné oblasti je
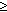 libovolnému prvku vlevo od něj (s
vyjímkou prvků z pomocné oblasti).
libovolnému prvku vlevo od něj (s
vyjímkou prvků z pomocné oblasti).
Důkaz:Ukážeme, že počet opačných inverzí libovolného z prvků vpravo od pomocné oblasti je po
5. kroku algoritmu 0, a tedy je příslušná část posloupnosti setříděná (protože každému prvku
předchází všechny prvky menší než on).
Zvolme libovolný prvek Ri vpravo od pomocné oblasti.
-
Předpokládejme, že se tento prvek vyskytnul při (některé iteraci) slévání běhů v prvním běhu.
Tento první běh končil prvkem tail(Bj ) takovým, že
tail(Bj ) > head(Bj+1 ), při čemž druhý běh
sestával pouze z bloku Bj+1 . Protože
tail(Bj ) > head(Bj+1 )
s využitím tvrzení 2.1 dostáváme, že všechny opačné inverze prvku tail(Bj )
pochází z bloku Bj+1 a tedy po slití těchto běhů se počet opačných inverzí
prvku tail(Bj ) změní na 0, tudíž i počet opačných inverzí prvku
Ri se změní na 0.
-
Pokud se prvek z Ri vyskytnul v 2. běhu při některé iteraci slévání a byl slit
(tedy nepřipadl do 1. běhu v další iteraci), pak Ri < než nejlevější prvek
prvního běhu - ten má ale počet obrácených inverzí 0 (viz výše) a tudíž i Ri
má počet obrázených inverzí 0.
Druhá část tvrzení je zřejmá - protože prvky vpravo od pomocné oblasti tvoří jediný běh, jsou
vzájemně vůči sobě uspořádané; jelikož všechny prvky vlevo od pomocné oblasti mají počet
obrázených inverzí = 0, žádný z nich není větší než libovolný prvek vpravo od pomocné oblasti.
- Tedy po provedení kroku 6. je posloupnost v B1 ... Bs-1
setříděna a blok Bs obsahuje s největších prvků celého pole. Ty setřídíme v kroku
7., čímž je úloha vyřešena.
Časová složitost:
Rozebereme jednotlivé kroky:
První krok zvládneme dle předpokladu (a jak je níže ukázáno) v čase O(s); druhý krok, tedy setřídění
bloků (obdobně jako v Kronrodově alg.) zabere čas O(s .(s + s)). 3. - 5. krok
algoritmu potřebuje v součtu přes všechny iterace čas 0(s) pro určování délky 1. běhu (2. běh triv.)
a O(n) pro slévání (každé porovnávání a přesun v této části algoritmu vyústí v konečné umístění 1
prvku). 6. krok zvládneme v čase lineárním k délce posunovaných posloupností - tedy určitě O(n) a 7.
krok v čase O(s2).
Tedy v celkovém součtu O(n).
- Nejdříve vyřešíme specielní případ, kdy délka jedné ze vstupních posloupností je
k <
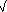 n. Bez újmy na obecnosti předpokládejme, že tato
"krátká" posloupnost je ta první, tedy
R1 ... Rk. V tomto případě lze slévání provést efektivně
pomocí metody "block merge forward" popsané v [Pardo].
n. Bez újmy na obecnosti předpokládejme, že tato
"krátká" posloupnost je ta první, tedy
R1 ... Rk. V tomto případě lze slévání provést efektivně
pomocí metody "block merge forward" popsané v [Pardo].
Porovnáme R1 a Rk+1 - je-li
R1 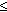 Rk+1 je R1 na své finální pozici.
Pokud R1 > Rk+1, najdeme prvek Rp takový,
že Rp < R1
Rk+1 je R1 na své finální pozici.
Pokud R1 > Rk+1, najdeme prvek Rp takový,
že Rp < R1 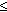 Rp+1 a pak všechny
prvky R1 ... Rp cyklicky posuneme ("rotace" - jak ji provést
v čase O(p) viz níže) o p - 1 pozic doprava - tedy
nejpravější prvek té "krátké" posloupnosti bude na p-té pozici v poli. Tento prvek
a všechny prvky vpravo od něj jsou nyní na svých finálních pozicích. Pokračujeme ve slévání -
iterujeme stejný postup pro oblast pole Rp+1 ... Rn. V okamžiku, kdy
všechny prvky jedné z původních posloupností budou na svých finálních pozicích, slévání je úspěšně
ukončeno.
Rp+1 a pak všechny
prvky R1 ... Rp cyklicky posuneme ("rotace" - jak ji provést
v čase O(p) viz níže) o p - 1 pozic doprava - tedy
nejpravější prvek té "krátké" posloupnosti bude na p-té pozici v poli. Tento prvek
a všechny prvky vpravo od něj jsou nyní na svých finálních pozicích. Pokračujeme ve slévání -
iterujeme stejný postup pro oblast pole Rp+1 ... Rn. V okamžiku, kdy
všechny prvky jedné z původních posloupností budou na svých finálních pozicích, slévání je úspěšně
ukončeno.
Celý tento postup zabere O(n), neboť "krátká" posloupnost má <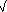 n
prvků a tedy její prvky se přesouvají nejvýše
n
prvků a tedy její prvky se přesouvají nejvýše 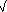 n-krát a každý prvek druhé posloupnosti
se posouvá nejvýše jednou.
n-krát a každý prvek druhé posloupnosti
se posouvá nejvýše jednou.
(V případě, že "krátká" posloupnost v poli následuje jako druhá, použijeme analogický
algoritmus začínající největším prvkem této "krátké" posloupnosti ("block merge
backwards").)
- Z předchozího tedy můžeme předpokládat, že každá ze vstupních posloupností má alespoň
s=
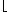
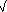 n
n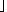 prvků.
Protože (s + 1)2 > n , víme, že počet bloků velikosti
s v poli je tedy nejvýše s + 2 .
prvků.
Protože (s + 1)2 > n , víme, že počet bloků velikosti
s v poli je tedy nejvýše s + 2 .
Pomocí porovnávání pravých konců posloupností najdeme s největších prvků, které budou ve
vlastním algoritmu sloužit jako pomocná (auxiliary) oblast - označme tyto 2 části posloupností
A a B s velikostmi po řadě s1 a s2
(s1 + s2 = s). Označme s2 prvků
nalevo od A jako C. Dále označme D nejkratší (třeba i prázdnou) skupinu prvků
nalevo od B takovou, že pokud bychom D a B odstranili z druhé vstupní
posloupnosti, její délka by byla celým násobkem čísla s.
Nyní tedy můžeme na pole nahlížet jako na posloupnost bloků velikosti s - s vyjímkou prvního
bloku o velikosti t1 a posledního bloku (D B) o velikosti
t2, kde 0 < t1 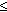 s a
0 < t2 < 2s. (A C má velikost s.)
s a
0 < t2 < 2s. (A C má velikost s.)
- Vyměníme B a C, čímž dostaneme pomocnou oblast do 1 bloku.
Nyní použijeme pomocnou oblast pro slití C a D (je-li některý prázdný, nic neděláme),
výsledkem tohoto bude blok E o velikosti t2 (stále na pravém konci pole).
Nyní můžeme rozlišit 2 případy:
- Délka E > s - v tomto případě byly C i D neprázdné a tudíž
všechny prvky od pozice s + 1 v E jsou
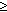 libovolnému prvku
nalevo od nich (i mimo E, ale s vyjímkou pomocné oblasti) a tedy v algoritmu se jimi vůbec
nemusíme zabývat, až při závěrečném posunu pomocné oblasti se nám posunou, čímž se dostanou
na své finální pozice. Tedy stačí se zabývat prvními s prvky - totožné s následujícím
bodem.
libovolnému prvku
nalevo od nich (i mimo E, ale s vyjímkou pomocné oblasti) a tedy v algoritmu se jimi vůbec
nemusíme zabývat, až při závěrečném posunu pomocné oblasti se nám posunou, čímž se dostanou
na své finální pozice. Tedy stačí se zabývat prvními s prvky - totožné s následujícím
bodem.
- Pokud je délka E
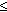 s a C i D byly neprázdné - pak
tail(E )
s a C i D byly neprázdné - pak
tail(E ) 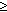 libovolnému prvku mimo pomocnou oblast a tedy při třídění bloků s
E nehýbeme a později ho normálně sléváme (že může být kratší nám nevadí).
libovolnému prvku mimo pomocnou oblast a tedy při třídění bloků s
E nehýbeme a později ho normálně sléváme (že může být kratší nám nevadí).
Byl-li některý z C, D prázdný, pak tail(E ) (a tedy i všechny
ostatní prvky v E) může být menší než některý z prvků v předcházejících blocích (opět se
nezabýváme prvky pomocné oblasti). To ovšem znamená, že všechny takovéto prvky se vyskytnou
v 1. běhu v okamžiku, kdy E bude 2. běh - protože všechny takovéto prvky musí pocházet
ze stejné vstupní posloupnosti a vzhledem k setřídění bloků (mimo E) dle jejich
tail(...), nikde za prvním takovýmto prvkem, ale před head(E ), nedojde k
přerušení tohoto běhu.
Tedy s tímto blokem v algoritmu normálně pracuji, s vyjímkou fáze třídění bloků, kdy ho
ignoruji - tedy nechám ho, kde je.
Tedy E mi v algoritmu žádné problémy nezpůsobí.
- Nyní nám tedy problémy může působit jen nejlevější blok (označme ho F) a to pouze za
předpokladu, že jeho velikost je < s. Označme G nejlevější blok druhé vstupní
posloupnosti. Použijeme t1 nejpravějších prvků pomocné oblasti pro slití bloků
F a G (stejným způsobem jako v algoritmu, tedy těch t1 prvků
pomocné oblasti se přestěhuje na začátek pole) - výsledné 2 bloky označme H a I.
Jelikož jsme slili 2 bloky obsahující nejmenší prvky každé ze vstupních posloupností, můžeme H
přesunout na začátek pole (tedy prohodit s tou částí pomocné oblasti, která zde do teď byla), kde
již zůstane až do konce algoritmu - obsahuje totiž setříděné nejmenší prvky celého pole. Tímto se nám
rovněž pomocná oblast spojí zpět do 1 bloku. S blokem I se bude v algoritmu pracovat jako s
každým jiným.
Nyní tedy vyměníme pomocnou oblast s prvním blokem následujícím za H, čímž jsme připraveni
pro spuštění výše uvedené zjednodušené varianty algoritmu. (Obsah zpracovávané části sice nesplňuje
zcela tam uvedené předpoklady, ale vše, co opravdu potřebujeme ano. Stačí přeskočit 1. krok
algoritmu a dát si pozor na to, že počet bloků nemusí přesně odpovídat velikosti bloků.)
- Časová složitost výše uvedených úprav vstupních posloupností:
1. krok lze triviálně provést v čase O(s), ve 2. kroku výměna i slití bloků zabere každé
O(s) a 3. krok zabere rovněž O(s).
Tedy celkem tyto úpravy zaberou čas O(s) a tedy nám časovou složitost algoritmu nezvýší.
Tento příklad byl převzat z [Huang, Langston].

Poznámky k algoritmu:
- Rotaci - tedy prohození 2 částí pole (označme je X a Y) lze
provést jednoduše v lineárním čase k počtu prvků těchto částí pole: Nejdříve obrátíme (tedy vyměníme
1. prvek s posledním, 2. prvek s předposledním atd.) X, pak obrátíme v celku X Y
(tím se nám prvky z X dostanou na požadovanou pozici) a na závěr obrátíme Y (které
před tímto krokem zabíralo začátek pole).
- Tento algoritmus (stejně jako Kronrodův) není stabilní (stable) - lze to snadno vypozorovat z
výše uvedeného příkladu.
- Autoři algoritmu v závěru článku ukazují (nepříliš šťastným způsobem, neboť výměnu dvou prvků a
jejich porovnání chápou jako stejně dlouho trvající operace, což nemusí být pravda, neboť prvky
mohou mít složitější strukturu a pro jejich porovnání mi může stačit jen jejich část - klíč), že
tento algoritmus by měl běžet v čase 3,5n + c pro nějakou konstantu c, zatímco
libolný slévající algoritmus musí běžet v čase alespoň 2n - 1.
- Autoři rovněž ukazují empirické výsledky, podle kterých je tento algoritmus při 5000 prvcích zhruba
dvakrát (a při 106 prvcích asi 1,75-krát) pomalejší než rychlé slévání používající
lineárně mnoho pomocné paměti. Pro detaily viz [Huang, Langston].
Shrnutí:
Oba výše uvedené algoritmy řeší danou úlohu. Druhý z nich je efektivnější a proto snad použitelný v
praktických aplikacích, kde je nepotřebnost více než konstantní pomocné paměti výraznou výhodou - půjde
tedy především o vnější třídění rozsáhlých souborů. Nicméně oba algoritmy jsou nestabilní (tedy
nezachovávají pořadí prvků se stejnou hodnotou klíče), což může v některých aplikacích vadit. Existuje ale
řada algoritmů řešících tuto úlohu, které jsou stabilní - příkladem může být [Pardo]
nebo [Huang, Langston 2].
Zdroje a literatura:
Zdroje jsou zvýrazněny tučně. Upozorňuji, že všechny důkazy v tomto článku jsem vytvořil sám, a tedy
nejsou obsaženy ani v [Knuth], ani v [Huang, Langston].
- [Kronrod] M. A. Kronrod: An ordering algothm without a field of operation.
(Dok. Akad. Nauk SSSR 186, str. 1256-8, 1969)
- [Knuth] D. E. Knuth: The art of computer programming - vol. 3: Sorting and
searching. (Addison-Wesley, 1973)
(Část týkající se slévání na místě v lin. čase: kapitola 5.2.4, příklad 18 - resp. jeho řešení na
konci knihy.)
- [Huang, Langston] B. C. Huang, M. A. Langston: Practical In-Place
Merging. (Communications of the ACM, March 1988, vol. 31, no. 3, str. 348 - 352)
- [Pardo] L. T. Pardo: Stable sorting and merging with optimal space and time bounds.
(SIAM J. Comput. 6, str 351 - 372, 1977)
- [Huang, Langston 2] B. C. Huang, M. A. Langston: Fast stable
merging and sorting in constant extra space (Computer Science Dep. Tech. Report CS-87-170, Washington
State University, 1987)
- Některé další práce na toto téma lze najít v
ResearchIndexu.
Tento článek smí být používán libovolně, za předpokladu, že nebude modifikován a že takto
bude učiněno se zmínkou o autorovi a odkazem na stránku
http://jt.sf.cz, odkud by měla být dostupná aktuální verse tohoto
článku.
Snažím se, aby informace zde uvedené byly pravdivé a pokud možno přesné, nicméně nenesu žádnou
odpovědnost za to, že tomu tak opravdu je, ani za jakékoli škody, které by někomu v důsledku případných
špatných či nepřesných informací z tohoto článku mohly vzniknout.
Jakékoliv dotazy či připomínky mi můžete poslat mailem.
Zpět na stránku referátů a jiných výtvorů
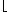
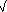 n
n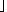 . Rozdělíme pole (obsahující zmíněné
posloupnosti) na bloky délky s, poslední blok (necelý) bude mít délku n mod s
(což může být 0). Označme počet celých bloků m + 1, bloky označme
B1 ... Bm, Bm+1, Bm+2 (kde
Bm+2 je ten necelý popř. prázdný blok).
. Rozdělíme pole (obsahující zmíněné
posloupnosti) na bloky délky s, poslední blok (necelý) bude mít délku n mod s
(což může být 0). Označme počet celých bloků m + 1, bloky označme
B1 ... Bm, Bm+1, Bm+2 (kde
Bm+2 je ten necelý popř. prázdný blok).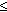 t < 2s . (A obsahuje právě prvky z bloku, který
obsahoval Rk a z bloku Bm+2 .}
t < 2s . (A obsahuje právě prvky z bloku, který
obsahoval Rk a z bloku Bm+2 .}
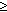 2), kde Bi
je první blok takový, že tail(Bi ) > head(Bi+1 ).
Druhý běh bude sestávat pouze z bloku Bi+1.
2), kde Bi
je první blok takový, že tail(Bi ) > head(Bi+1 ).
Druhý běh bude sestávat pouze z bloku Bi+1.



