Josef Troch (troch@mail.ru)
29.8.2000 (poslední změna 8.11.2000)
Algoritmy LZFG
Pojmem LZFG se označuje několik příbuzných komprimačních algoritmů, které vyvinuli
Edward Fiala a Daniel Greene roku 1989. Tyto algoritmy jsou bezztrátové
a adaptivní - jsou to slovníkové metody, které jsou v podstatě "kříženci"
mezi metodami LZ 77 a LZ 78. Z tohoto důvodu se o těchto metodách krátce zmíním.
LZ 77 i LZ 78 jsou nazvány dle svých autorů - Abraham Lempel a Jacob Ziv
a roku uveřejnění.
První (a účinnější) z těchto metod - LZ 77 - funguje na principu
tzv. posuvného okna (sliding window) - toto je rozděleno na dvě části: prohlížecí okno
(search buffer) a aktuální okno (look-ahead buffer). Prohlížecí okno je na začátku
prázdné a v aktuálním je začátek dat, která chceme komprimovat - posuvné okno se pak
posouvá "směrem doprava" - tedy prohlížecí okno se zaplňuje tím co bylo v
aktuálním a do aktuálního se načítají nová data. Vlastní komprese probíhá tak, že se
snažíme najít co nejdelší předponu slova v aktuálním okně, která je shodná s nějakým
slovem, které začíná v prohlížecím okně. Tuto zakódujeme trojicí
[i, j, k], kde i je vzdálenost začátku nalezeného slova
v prohlížecím okně od začátku aktuálního okna, j je délka zmíněné předpony, a
k je první znak následující za touto předponou (tedy pro triviální předponu
[0, 0, k] ). Posuvné okno posuneme o j+1 znaků doprava.
Dekomprese je zde trivialní -
kopíruje příslušné řetězce (po znacích - kvůli slovům, která zasahují do (ještě neznámého)
aktuálního okna), přidává za ně příslušný znak k a posunuje okno.
Slovníkem je zde tedy prohlížecí okno. U této metody je bohužel dosti pomalá komprese
(při klasické implementaci), narozdíl od metody LZ 78.
Metoda LZ 78 si vytváří slovník explicitně v paměti - tento je na začátku prázdný.
Ze vstupu načteme nejdelší frázi f, která je již ve slovníku a jeden znak po ní
následující - označme ho z. Na výstup pak zapíšeme dvojici [i ,z],
kde i je ukazatel (číslo řádku) do slovníku na frázi f. Do slovníku je
pak přidána fráze fz.
Při zaplnění slovníku je třeba nějak ho reorganizovat - třeba smazáním celého slovníku.
Dekomprese je zde také jednoduchá - dekompresor si totiž vytváří slovník, který je v každém
okamžiku stejný se slovníkem kompresoru a tak dle načtených dvojic snadno rekonstruuje
původní data.
Tento algoritmus je sice rychlejší, ale v typickém případě má o něco horší kompresní
poměr než LZ 77.
Všechny metody třídy LZFG jsou založeny na následující myšlence: enkoder generuje komprimovaný
soubor obsahující dva druhy dat "tokeny" a ASCII kódy znaků (literály).
Tokeny mohou být dvojího druhu: literal token ("znakový") a copy token ("kopírovací").
Literal token v komprimovaném souboru znamená, že teď následuje řetězec literálů (ASCII kódů)
- tedy objeví-li se v komprimovaném souboru "(literal x)"
znamená to příkaz pro dekompressor - načti x znaků z komprimovaného souboru a
zapiš je přímo na výstup (dekomprimovaný soubor).
Copy token ukazuje na řetězec, který už se objevil ve zpracovávaných datech
- přesněji: objeví-li se v komprimovaném souboru "(copy x, y)" říká
to dekompresoru, aby se vrátil o y znaků ve výstupním (dekomprimovaném)
souboru a zkopíroval odtud x znaků na konec výstupního souboru.
Příklad:
Z řetězce "the_boy_on_my_right_is_the_right_boy" po zakódování může vzniknout:
"(literal 23)the_boy_on_my_right_is_(copy 4, 23)(copy 6, 13)(copy 3, 29)"
Dosažená komprese závisí mimo jiné na tom, jakým způsobem budeme zapisovat
(tedy kolik místa zaberou) literal a copy tokeny.
Metoda A1
Metoda A1 je nejjednodušší metoda třídy LZFG.
Používá 8 bitů pro literal token a 16 bitů pro copy token.
Rozlišení a formát tokenů:
- Pokud jsou první 4 bity nulové, pak tento kód je kódem literal tokenu a další 4 bity
kódují délku řetězce x v rozmezí [1..16]. Za tímto kódem tedy musí následovat
x kódů ASCII znaků.
- V opačném případě (alespoň jeden z prvních 4 bitů nenulový) se jedná o kód
copy tokenu a první 4 bity udávají délku x v rozmezí [2..16] a
dalších 12 bitů je vzdálenost y (odkud kopírovat) v rozmezí [1..4096].
Kompresor i dekompresor používají posuvné okno podobně jako algoritmus LZ 77 (viz výše),
ovšem toto bude jinak reprezentováno pro urychlení komprese.
V každém kroku se kompresor rozhoduje, zda zapíše literal token či copy
token tímto způsobem:
- Pokud je kompresor v "počátečním" stavu (právě dokončil copy token nebo
ukončil literal token kvůli limitu na 16 znaků či jde o úplný začátek komprese):
- Pokud nejdelší shoda (s předponou slova v aktuálním okně), kterou se
kompresoru podaří najít (v prohlížecím okně) je délky alespoň 2, bude zapsán
copy token.
- Jinak začneme zapisovat literal token.
- V opačném případě (tedy kompresor je někde uprostřed zapisování literal tokenu)
literal token budeme prodlužovat dokud neobjevíme shodu délky alespoň 3, nebo dokud
nedosáhneme délkového limitu na délku literal tokenu (16).
Pozn.: Zapsáním literal tokenu myslím samozřejmě zapsání vlastního tokenu (= 8 bitů) +
zapsání příslušných ASCII kódů.
Příklad:
Algoritmus A1 tedy zakóduje text z předchozího příkladu takto:
"(literal 16)the_boy_on_my_ri(literal 7)ght_is_(copy 4 23)(copy 6 23)(copy 3 29)"
Algoritmus A1 je podobný metodě LZ 77, ale liší se mimo jiné použitím specielního
literal tokenu. Empirické studie autorů algoritmu ukázaly, že pro anglický text a
zdrojové soubory lze mírně zlepšit kompresní poměr zmenšením maximální délky v literal
tokenu o 1 bit. Tímto ovšem přijdeme o možnost práce se souborem po bytech (literal
token by byl 7 bitů).
Algoritmus A1 byl vytvořen na kompresi 8 bitového textu, ale ukazuje se jako celkem vhodný i na
ostatní druhy dat.
Datové struktury pro algoritmus A1
Aby bylo možno najít nejdelší shodu (viz výše) co nejrychleji (tedy aby byl celý
algoritmus rychlý) je nutno použít netriviální datové struktury.
Tedy máme posuvné okno pevné délky a sestavíme pro něj strom, obsahující všechny
přípony slova v tomto okně (suffix tree).
Pro algoritmus A1 se používá modifikace struktury zvané McCreight`s suffix tree,
která je sama modifikací Morrisonova PATRICIA tree, který je založen na datové struktuře
zvané Trie.
Trie je stromová struktura, kde větvení nastává podle "pozic" klíče
(místo dle porovnání mezi klíči) - zde "pozice" = písmeno - tedy v hloubce
l ve stromu bude docházet k větvení podle l-tého písmene slov ve stromu.
Každá hrana tedy odpovídá právě 1 písmenu a každý vrchol reprezentuje řetězec, který
získáme na cestě z kořene do tohoto vrcholu. Příklad: budeme-li chtít sestrojit strom
obsahující jediné slovo délky 20, bude mít hloubku 20 (bude to cesta).
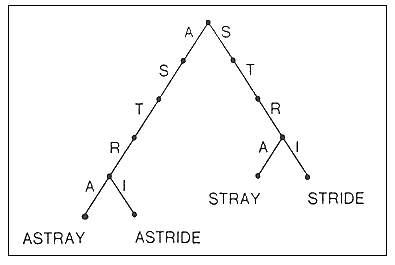
Obrázek 1
Výše uvedený obrázek zobrazuje Trie pro 4 slova. Je zjevné, že mnoho vnitřních
uzlů tohoto stromu je nadbytečných, neboť mají jen jednoho syna.
Pokud chceme vytvořit slovník pro nějaký soubor, ušetříme místo, odstraníme-li
nadbytečné vnitřní uzly a použijeme-li ukazatele do souboru místo ukládání všech
příslušných znaků v datové struktuře. Tímto dostáváme v podstatě Morrisonův PATRICIA
tree, který je zobrazen na níže uvedeném obrázku.
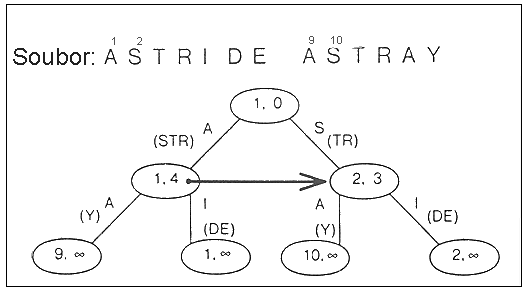
Obrázek 2
K obrázku 2:
- Řetězce v závorkách nejsou reprezentovány přímo v datové struktuře, ale
mohou být získány z dvojic [position,level] v uzlech.
- Position označuje, na které pozici v souboru začíná slovo reprezentované na
obrázku celou cestou od kořene.
- Level udává kolik písmen se má použít pro vytvoření příslušného slova
(Pozn.: všechny listy odpovídají slovům, která začínají
na různých místech v souboru, ale pokračují až do konce souboru)
- Tučná šipka na obrázku znázorňuje "suffix pointer", o kterém se
zmíním později
Protože pro nás pozice odpovídají bytům, uzel ve stromě může mít až 256 synů. Jelikož
256 synů téhož listu se objeví jen zřídka, nevyhradíme na ně místo, ale raději použijeme
hašování.
Pro algoritmus A1, potřebujeme vždy najít nejdelší (maximálně 16 znaků)
shodu s řetězcem v aktuálním okně, která začíná na kterékoli z předchozích
4096 pozic.
Pokud všech předchozích 4096 řetězců bylo uloženo do PATRICIA tree s hloubkou
d=16 (což zajistíme - viz dále),
nalezení této shody je triviální (přímý průchod stromem od kořene).
Bohužel vkládání těchto řetězců může být časově náročné (Pokud jsme pro vložení
řetězce začínajícího na pozici i prošli přes d pater stromu, při vkládání
řetězce z pozice i+1 projdeme alespoň do hloubky d-1. Což vede k časové
složitosti O(n.d) v nejhorším případě (n je délka souboru).).
Protože v dalších algoritmech bude d výrazně větší než 16, je třeba ho
odstranit z časové složitosti výpočtu.
Pro vkládání řetězců v čase O(n) McCreight přidal do PATRICIA tree
"suffix pointery". Tedy každý vnitřní vrchol stromu, reprezentující
řetězec aX na cestě z kořene do tohoto vrcholu, má pointer na vrchol
reprezentující X (tedy řetězec získaný z aX odstraněním prvního písmene).
Pokud byl v předchozím kroku přidán řetězec začínající na i-té pozici v
souboru do hloubky d ve stromě, není třeba se vracet do kořene stromu pro
přidání řetězce začínajícího na i+1 - místo toho použijeme suffix pointer,
který nás dovede k příslušnému uzlu v hloubce d-1, odkud pokračujeme klasicky
(procházením stromu).
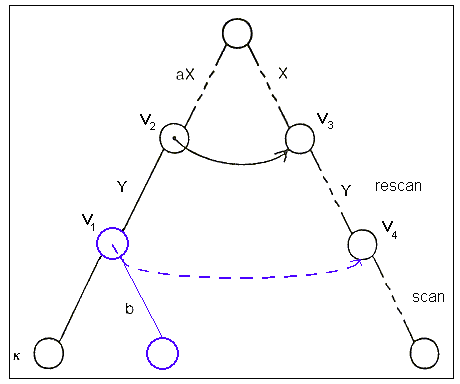
Obrázek 3
Výše uvedený obrázek ukazuje vytváření a používání suffix pointerů.
Předpokládejme, že v předchozím kroku jsme nalezli maximální řetězec shodující se
(s aktuálním řetězcem) aXY, kde a je jeden znak, X a Y
jsou řetězce a b je první neshodující se znak za Y (ze vstupu).
Obrázek 3 ukazuje komplikovaný případ, kde byl do stromu přidán nový vnitřní
vrchol (v1) a je třeba pro něj vytvořit suffix pointer.
Následující řetězec XYb přidáme tak, že jdeme z v1 do
jeho otce (v2 - odpovídá aX), pak následujeme příslušný
suffix pointer do v3 (odpovídá X), odtud sestupujeme hlouběji
do stromu - nejprve znovu dle řetězce Y ("rescanning") do
v4, pak z něj dolů, čímž se přidá nový řetězec. Název
"rescanning" vychází z toho, že se pohybujeme dle části řetězce, která byla
použita už při předchozím přidání fráze a tak není nutno porovnávat řetězce na hranách
(stačí písmena přímo v dat. struktuře a údaje o délce) - což potřebujeme pro lineární
časovou složitost.
"Rescanning" skončí buď v již existujícím uzlu v4 (ten má
suffix pointer) nebo v uzlu v4, který musí být vytvořen kvůli vložení
XYb (XYb bude odpovídat vrcholu, který bude synem v4) - pro
tento nový uzel ovšem
suffix pointer vytvoříme v další iteraci (přidávání další fráze).
Tedy každý uzel (kromě posledního vytvořeného) má suffix pointer.
Protože algoritmus A1 má pevnou velikost prohlížecího okna (4096 bytů), potřebujeme
být schopni vymazávat části stromu, odpovídající řetězcům, které začínají dále
než před 4096 byty v souboru.
Z tohoto důvodu je třeba k naší stromové struktuře něco přidat:
- Listy stromu dáme do cyklického bufferu (fronty), takže bude snadné identifikovat
a odstranit nejstarší list.
- Vnitřním vrcholům přidáme položku "počet synů". Když nějakému
vnitřnímu vrcholu tato položka klesne na 1, tento vrchol smažeme a z hrany
vedoucí do tohoto vrcholu a z hrany vedoucí z tohoto vrcholu vytvoříme hranu
jedinou.
Lze ukázat, že výše uvedené odstanění vnitřního uzlu nikdy nezpůsobí to, že
by nějaký existující suffix pointer ukazoval na tento (již smazaný) uzel.
Bohužel tím, že jsme odstranili nutnost vracet se do kořene při každém přidání fráze,
mohlo by se stát, že se budeme stále pohybovat jen ve "spodních částech"
určitých podstromů ("větvích") stromu a pointery ("position") v jejich částech blížších
ke kořeni se stanou zastaralými (t.j. budou ukazovat na řetězce již za levým okrajem
prohlížecího okna). Procházení stromu po "větvi" vždy až ke kořeni by také
nebylo řešením - přišli bychom o všechny výhody suffix pointerů.
Lze udržet pointery platné bez nutnosti časově náročných updatů pomocí
"častečné" aktualizace (updatu) při každém přidání fráze.
- Každému vnitřnímu uzlu přidáme "update bit".
- Pokud je update bit=1 při aktualizaci uzlu, změníme update bit na 0 a
pokračujeme v aktualizaci (rekursivně) u otce tohoto uzlu.
- V opačném případě (update bit=0 při updatu uzlu), změníme update bit na 1 a
skončíme s aktualizací pointerů.
Spočítáme-li čas potřebný k updatu pointrů přes všechny nové listy, zjistíme, že na
každý list vychází 2 updaty. Tyto "částečné" updaty budou mít za výsledek
udržení všech pointerů na posledních 4096 bytech v souboru což je to, co jsme
potřebovali. Důkazy obou výše zmíněných faktů lze nalézt ve Fialově a Greenově článku
(str. 493).
Shrnutí operací jednoho kroku (přidání fráze) algoritmu (dle obrázku 3):
- Máme vytvořen list v1
- Použijeme suffix pointer otce uzlu v1 k nalezení uzlu
v3.
- Odtud jdeme ve stromě dolů do v4 (rescanning - máme hledaný suffix pointer) a pak
"scanning".
- Odtud provedeme částečný update (pohybujíce se směrem ke kořeni) - nastavujeme
"position" na aktuální pozici v souboru a nastavujeme update bity
na 0, dokud nenajdeme uzel, jehož update bit je roven 0.
- V cyklickém bufferu listů nahradíme nejstarší list novým listem.
- Pokud otec (označme ho p) nejstaršího listu má teď pouze jediného syna,
musí být p rovněž smazán a zbylý syn je připojen k bývalému otci vrcholu
p.
Pak provedeme částečný update začínajíce s pozicí smazaného vnitřního
uzlu s tím rozdílem, že v každém kroku porovnáme pozici, kterou propagujeme z
dola s pozicí, která už ve zkoumaném uzlu je a s tou novější z nich pokračujeme
výše do stromu (tedy vůbec nepoužíváme aktuální pozici v souboru).
Jednodušší datová struktura pro A1
Vzhledem k tomu, že implementace algoritmu A1 pomocí výše uvedených datových struktur
je komplikovaná a tyto datové struktury mají dosti velké paměťové nároky, uvádí Fiala
a Greene ještě jednu variantu.
Tato varianta vychází z předchozích datových struktur (tedy z PATRICIA tree +
cyklický řešená fronta listů), ale používá jednodušší metody na nalezení přípony (suffixu) při vkládání
nové fráze a pro updatování položky "position" (tedy ukazatele do souboru) v
uzlech (kvůli posunům prohlížecího okna).
Místo "částečných" updatů lze updatovat položku "position" ve
všech uzlech na cestě nahoru do kořene, pokaždé, když přidáme nový list. Tímto se
zbavíme nutnosti jakýchkoli aktualizací, když uzly mažeme. Zároveň můžeme odstranit
update bity (už nejsou potřeba).
Alternativa k suffix pointerům už je složitější. Časová náročnost pohybu po
stromě není vždy stejná - pohyb dolů vyžaduje nahlédnutí do hašovací tabulky, což trvá
déle než použití ukazatele ze syna na otce. Proto rozumná cesta k nalezení potřebné
přípony (z uzlu odpovídajícího aX chci nalézt uzel odpovídající X , a - znak, X -
řetězec) je nalézt "suffix leaf" - tedy list reprezentující slovo, jehož
nějaká předpona je hledanou příponou (X) a odtud postupovat po ukazatelích na otce směrem
nahoru ke kořeni, dokud nenajdeme uzel odpovídající hledané příponě (tedy místo, kam
by směřoval suffix pointer, kdyby zde byl).
Zbývá problém, jak nalézt "suffix leaf". To ovšem není tak obtížné -
víme, že řetězec na pozici i v prohlížecím okně (aX) se shoduje (myslím
nejdelší shodu předpon - jako výše) s řetězcem na nějaké předchozí pozici j v
prohlížecím okně - tedy hledaný "suffix leaf" je položka následující za
listem odpovídajícím j ve frontě listů.
Pozn.: Tato fronta musí být řešena jako pole (pro rychlý přístup) - tedy bude se zde měnit
začátek této fronty (bude "cyklicky běhat" po poli) - hledaný
list najdeme přičtením j+1 k začátku fronty, pak výsledek mod 4096.
Metoda A2
Velikost prohlížecího okna 4096 bytů je (zhruba) optimální pro copy a literal tokeny
pevné délky (8b, 16b). Zvětšíme-li velikost prohlížecího okna, bude možno zvýšit
velikost kopírovaných dat u copy tokenů (objeví se shody větší délky), ale toto
vynutí zvětšení prostoru pro uložení vzdálenosti v copy tokenu.
Pro dosažení vyšší komprese je při použití většího okna vhodné použít kódování
čísel s proměnnou délkou zápisu (variable-width encoding), které bude vycházet z
toho, že bližší pozice v okně budou častěji používány v copy tokenech než pozice
vzdálenější.
Fiala a Greene dospěli k názoru, že bude nejlépe použít vhodnou kombinaci binárního
a unárního kódu a zavádějí start-step-stop kódy.
Start-step-stop kódy
Tyto kódy mají tento formát: začínají unárním kódem jakéhosi čísla n (tedy
n jedniček), pak následuje jedna 0 a pak binární číslo délky
start+n.step bitů. Čísla n probíhají od 0 do
(stop-start)/step.
Pokud délka zmíněného binárního čísla je právě stop bitů, závěrečná 0 za unárním
kódem se vynechává.
Mějme start-step-stop kód nějakého čísla x : unární kód mi tedy udává délku
následujícího binárního kódu a tento binární kód po přičtení počtu všech čísel s
kratším kódem (než je kód x) dává "normální" vyjádření čísla
x.
Těmto kódům jsou přirozená čísla (včetně 0) přiřazena sekvenčně (tedy nejmenší čísla mají nejkratší kódy).
Uvádím příklad pro (3, 2, 9) kód:
| n |
kód |
rozsah |
| 0 |
0xxx |
0-7 |
| 1 |
10xxxxx |
8-39 |
| 2 |
110xxxxxxx |
40-167 |
| 3 |
111xxxxxxxxx |
168-679 |
Tedy příslušný start-step-stop kód pro 7 bude 0111 a pro 10 bude 1000010.
Uvádím ještě jednoduchou funkci v programovacím jazyce C na výrobu
start-step-stop kódů - tato volá 2 jednoduché funkce - zapisbit(x) (která
zapíše 0, je-li x rovno 0, jinak 1) a zapbin(x, p) (která zapíše
x jako binární číslo o p bitech):
void sss(int start,int step,int stop,int cislo)
//start, step, stop: jaky kod pouzit; cislo: cislo k zakodovani
{int k=start;
while (cislo>=(1<<k)) //(1<<k) je jiny zapis pro 2 na k
//zde kontroluji, zda se cislo vejde uz do teto
{zapisbit(1); //skupiny kodu, jinak zvetsuji n
cislo-=(1<<k);
k+=step;
} //mam prislusny unarni kod
if (k!=stop) zapisbit(0);
putchar(':');
zapbin(cislo,k); //zapisu prislusne binarni cislo
}
Algoritmus A2 je slovníková metoda, podobná algoritmu A1.
K ukládání délky shodujícího se řetězce v copy tokenu používá (2, 1, 10)
start-step-stop kód, který umožňuje, aby délka tohoto řetězce byla až 2044 znaků
(kódy jsou o 1 posunuty, protože nepotřebujeme kód pro délku 1; tedy 001 znamená 2 atd.).
Kód 000 je vyhrazen pro signalizaci, že jde o
literal token. Pro kódování délky následujícího řetězce literálů (ASCII kódů)
je použit (0, 1, 5) kód, tedy maximální délka tohoto řetězce je 63 znaků.
Pokud tedy první 3 bity tokenu nejsou 000, jde o copy token a následuje odkaz na
příslušnou pozici v okně zapsaný (10,2,14) kódem, což nám umožní
velikost okna až 21504 bytů.
Pro rozhodování mezi copy tokenem a literal tokenem je zvolena stejná strategie
jako u algoritmu A1.
Jsou zde ještě tři drobná vylepšení, která algoritmus A2 používá
pro zlepšení komprese (dle Fialy a Greena o 1 - 2 %)
- Protože za řetězcem literálů kratším než maximální možná délka (63) nemůže
následovat ani další literal token, ani copy token délky 2, posuneme kód délky v
následujícím copy tokenu o 2 dolů - tedy kódy 000, 001, 010 budou znamenat shodu v
3, 4, 5 znacích (místo literal, 2, 3). Tímto způsobem se zvětší (ve výše uvedeném
případě) maximální zakódovatelná délka v copy tokenu na 2046 bytů.
- Jelikož pro kódování začátků souborů, či souborů krátkých nepotřebujeme
velikost okna celých 21K, použijeme pro ukládání odkazu na pozici v
copy tokenu kód se vzrůstající délkou, tedy
(10 - x, 2, 14 - x) kód, kde
x je na začátku 10 a klesá až na 0 podle toho, jak se prohlížecí okno postupně
zaplňuje.
Tedy kód, kde x = 10 (který se použije na začátku) má 21 hodnot, v
okamžiku, kdy počet znaků v okně (tedy platných pozic) přesáhne 21, snížíme x
na 9 atd.
Je dobré si uvědomit, že toto vylepšení se použije jen na začátku komprese, dokud celé
21K velké okno není zaplněno - výrazné zkrácení se tedy projeví jen u malých
souborů.
- Každý z výše uvedených kódů je schopen adresovat pevný počet pozic (od 21
pro x=10 po 21504 pro x=0). Pokud ještě okno není zcela zaplněno, či
uživatel se rozhodne použít prohlížecí okno menší velikosti, nejdelší z kódů by
nebyly nikdy použity (protože by to byly odkazy na neplatné pozice v prohlížecím okně
- t.j. zatím nezaplněné, či při menší velikosti okna pozice za levým okrajem okna).
Z tohoto důvodu se zde používá fázování při zápisu binární části
start-step-stop
kódu odkazu na pozici. Tedy místo zapsání všech hodnot k-bitově, nižší hodnoty
jsou zapsány jako kratší (k-1 bitová) čísla a vyšší hodnoty jako k
bitová.
Přesněji (už jen pro binární čísla) - potřebujeme-li používat čísla 0..p-1, kde
2k-1 < p < 2k,
číslo i zapíšeme takto: je-li
i < 2k - p, použijeme
k - 1 bitový binární kód čísla i; v opačném případě použijeme
k bitový binární kód čísla
i + 2k - p.
Příklad: uživatel se rozhodne používat prohlížecí okno velikosti 16384 B, tedy
je nutno použít (10, 2, 14) kód ( (9, 2, 13) kód má jen 10752
hodnot). Tento má 21504 hodnot, tedy nejdelších 5120 by nebylo nikdy použito.
Poslední skupina kódů ("11" následováno 14 bitovým číslem) má 16384 různých
hodnot, ze kterých by se použilo jen prvních 11264.
Místo toho budeme zapisovat prvních 5120 z nich jako "11" a 13 bitové číslo
a zbylých 6144 jako "11" a 14 bitové číslo.
Všechna tato 3 vylepšení povedou jen k velmi malému zvýšení komprese za cenu výrazně
pomalejšího kódování.
Datové struktury pro algoritmus A2
Je možno použít obě datové struktury uvedené u algoritmu A1, ale každá z nich má své
nevýhody, které zde uvádím.
První datová struktura (se suffix pointery a "částečnými updaty")
by se zdála být výhodnější kvůli velké maximální délce řetězce v copy tokenu, která
je zde až 2044 (2046).
Bohužel způsob aktualizace pozic (pointerů do okna) zde nezaručuje, že
ve struktuře bude uložena vždy nejbližší pozice shodujícího se řetězce, proto se může
občas stát, že budou použity v copy tokenech delší kódy pozice, než by bylo nezbytné.
Tento problém ovšem není až tak vážný, neboť strom často nemá příliš velkou hloubku
a uzly blízko kořene mají obvykle mnoho synů, takže updaty postupují stromem směrem
ke kořeni celkem rychle.
Druhá (jednodušší) datová struktura, kde probíhají updaty vždy až
ke kořeni, může na určitých ("nevhodných") datech fungovat až 20
krát pomaleji, ale dosáhne optimálního výsledku (pokud jde o kompresní
poměr).
Autoři uvádí, že na běžných souborech komprese algoritmu užívajícího datovou
strukturu se suffix pointery je asi o 0,4 % horší než u algoritmu
využívajícího jednodušší datovou strukturu.
Metody B1 a B2
Algoritmus A2 má velmi rychlou dekompresi s minimálními nároky na paměť, ale komprese
ačkoli probíhá v lineárním čase (vzhledem k délce souboru) je asi 5 krát pomalejší
než dekomprese. Algoritmy A1 a A2 jsou tedy vhodné pro použití v případech, kdy není
nutná maximální rychlost.
Rychlejší metody, označované jako B1 a B2 byly vyvinuty pro
archivaci souborů, kde, dle názoru autorů, metody A1 a A2 jsou příliš pomalé.
Metody B1 a B2 vychází po řadě z metod A1 a A2 (používají
stejné způsoby kódování pro copy a literal tokeny, tedy u B2 všechna 3 vylepšení uvedená
u metody A2 (kód (10 - x, 2, 14 - x), fázování, posunutí
po literálu kratším než 63 znaků)), ale počítají odkazy na
pozice do prohlížecího okna (pro copy tokeny) odlišně.
Tyto odkazy na pozice mohou ukazovat jen na místo, odpovídající
začátku řetězce, který byl zakódován nějakým předchozím copy tokenem nebo
na místa, která byla zapsána pomocí literal tokenu (klidně i doprostřed řetězce
literálů).
To znamená, že zde již nelze adresovat všechny pozice v prohlížecím okně.
Výše uvedeným se tyto algoritmy blíží metodě LZ 78.
Pozn.: Pozice v okně, počítané tímto
způsobem jsou označovány jako "compressed displacements" (stlačená
nahrazení / lépe: stlačené počáteční pozice), asi proto, že tímto dojde k
výraznému zvětšení prohlížecího okna a místa, kde mohou copy tokeny začínat jsou
"stlačena" k sobě, jako by okno bylo výrazně menší (tedy pro okno délky
200 KB bude třeba jen 16384 počátečních pozic - což by u A1 a A2 odpovídalo oknu
velikosti 16 KB). Počáteční pozicí myslím pozici, kam může "ukazovat"
copy token.
Délka v copy tokenu je stále udávána v počtu znaků (jako A1 a A2).
Zavedením tohoto způsobu číslování pozic v okně se rychlost komprimace zhruba
ztrojnásobí, ovšem rychlost dekomprese a rychlost, jakou se algoritmus adaptuje na
příchozí data se o něco sníží.
Datové struktury pro B1 a B2
Vzhledem k výše uvedenému způsobu číslování pozic v prohlížecím okně stávají se suffix
pointery a "částečné updaty" zbytečnými, tedy vhodnou datovou strukturou
je jednodušší PATRICIA tree. Nové položky jsou do slovníku vkládány jen na
"hranicích" řetězců odpovídajících tokenům (copy tokeny + literály) (vstupní
data jsou vlastně rozdělena na disjunktní řetězce a každý z nich se do slovníku
přidává právě jednou), což lze provést jednoduše v lineárním čase tak, že každou
iteraci začneme u kořene a procházíme dolů.
Je užitečné vytvořit pole "permanentních" uzlů (tedy tyto se nebudou v
průběhu času rušit) pro všechny znaky (odpovídají hloubce 1 ve stromě). Protože copy
token nikdy nemůže ukazovat na řetězec délky 1, nemusí nám vadit, že výše zmíněné
permanentní uzly nebudou odpovídat žádné pozici v prohlížecím okně.
Tedy každá iterace začíná indexováním do tohoto pole, pak nahlédnutím do hašovací
tabulky a porovnáváním se znaky na hranách stromu sestupujeme hlouběji do stromu
(jako u A1). Nová pozice prohlížecího okna je zapsána do vrcholů při tomto pohybu
stromem dolů, čímž je vyřešena aktualizace pozic ve stromě.
Tímto jsme se tedy zbavili všech komplikací nutných pro dosažení lineární časové
složitosti u algoritmu A2.
Bohužel, jedna nová komplikace se objevila: 16384 pozic v prohlížecím okně algoritmu
B2 (u B1 je tentýž problém, jen počet pozic je nižší) může odpovídat prohlížecímu
oknu dlouhému miliony znaků (což nemůžeme dovolit, nemáme nekonečně velkou paměť).
Autoři tedy zvolili za limit velikosti prohlížecího okna 12 . 16384 znaků.
Pokud velikost okna přesáhne tento limit, listy pro nejstarší pozice v okně jsou ze
stromu odstraněny (viz výše u algoritmu A1).
Dekompresor si nemusí udržovat PATRICIA tree, aby zjišťoval jakým
pozicím odpovídají "stlačené pozice" které získává z komprimovaného souboru.
Na toto mu stačí "přečíslovávací tabulka" - obyčejné pole, kam přistoupí
pomocí "stlačené pozice" jako indexu a získá "normální" pozici do
prohlížecího okna (tabulku si musí ovšem aktualizovat - po zaplnění prohlížecího okna v
každé iteraci přepíše její nejstarší položku).
Výsledky metod B1 a B2
Protože se algoritmus B2 pomaleji přizpůsobuje měnícímu se charakteru vstupních dat,
obvykle malé soubory komprimuje o něco hůře než algoritmus A2. Ale na textových
souborech a zdrojových souborech programů dosahuje B2 asymptoticky o 6 - 8 % lepších
výsledků než A2; přelom od horší komprese k lepší (porovnáváno s A2) nastává zhruba
po 70000 znacích. A2 je schopen lépe zachytit blízký kontext, B2 je schopen (kvůli
"compressed displacements") odkázat dále zpátky do souboru. Toto je pro B2
výhoda na souborech s "přirozenou strukturou slov", jako jsou textové
soubory, a nevýhoda na souborech, kde je obzvlášť důležitý blízký kontext, jako jsou
naskenované fotografie.
Fiala a Greene rovněž zkoušeli varianty, kdy jsou fráze do stromu přidávány
častěji než po každém znaku zapsaném jako literál a na hranici copy tokenů.
Všechny tyto metody (včetně A2) mohou být implementovány podobně jako B2, pokud se
nezajímáme o rychlost komprese.
Například, o jedno procento lepší komprese lze prý dosáhnout vložením jedné počáteční
pozice (tedy pozice, na kterou může ukazovat copy token) mezi každé 2 znaky
reprezentované copy tokenem, odkazujícím na řetězec délky 2 (dále jen copy token
délky 2). O další 0,5 % lze kompresi zlepšit přidáním počátečních pozic za každý znak,
odpovídající copy tokenu délky 3.
Ale protože tyto změny zpomalují kompresi i dekompresi, žádný z algoritmů třídy LZFG
je nevyužívá.
Metoda C2
Narozdíl od metod B1 a B2, metoda C2 byla vytvořena za účelem zlepšení kompresního
poměru na úkor rychlosti algoritmu.
Pokud se nějaký řetězec objevuje v souboru často, žádná z výše uvedených metod
nefunguje optimálně, neboť když komprimují tento řetězec, existuje několik
různých pozic v okně, na které může pozice z copy tokenu ukazovat, ačkoli (při
dekompresi) je třeba zkopírovat jen jeden řetězec.
Ale datové struktury, které používáme, místem neplýtvají - opakující se řetězce
odpovídají stejné cestě z kořene. Založíme-li tedy kódová slova pro kopírování
řetězce (copy tokeny) na datové struktuře slovníku, znatelně zlepšíme kompresní poměr.
(Kódovými slovy založenými na pozicích v explicitním slovníku se tato metoda blíží
metodě LZ 78, ačkoli prohlížecím oknem a explicitním udáváním délky kopírovaného
řetězce připomíná metodu LZ 77.)
Metoda C2 používá pro uložení slovníku stejnou datovou strukturu jako
metoda B2 (PATRICIA tree), rovněž shodně používá metodu "compressed
displacements" k číslování pozic v okně.
Abychom mohli udat pozici řetězce ve slovníku, je třeba udat 2 informace: číslo
uzlu a umístění na hraně mezi zmíněným uzlem a jeho otcem (protože tato hrana může
odpovídat řetězci delšímu než 1 znak).
Listy a vnitřní vrcholy očíslujeme každé zvlášť. Při volbě kódového slova pro
kopírování řetězce z prohlížecího okna rozlišíme 2 případy:
Pokud příslušná hrana (viz výše) končí v nějakém listě stromu, použijeme
kódové slovo "LeafCopy", v opačném případě (hrana vede mezi vnitřními
vrcholy stromu), použijeme kódové slovo "NodeCopy".
Tedy zmíněné řetězce opakující se v prohlížecím okně jsou zakódovány pomocí NodeCopy.
Abychom rozlišili kódová slova, musí být před každým z nich bitový příznak
(flag) - 0 pro NodeCopy, 1 pro LeafCopy či literál (literal token).
V kódovém slovu pro NodeCopy je flag následován číslem příslušného
(vnitřního) vrcholu (počet vnitřních vrcholů bývá zhruba 50 % počtu listů).
Za číslem vrcholu následuje délka řetězce podél hrany z otce zmíněného
vrcholu (tedy jak dlouhý úsek této hrany se má použít pro získání řetězce při
dekompresi). Protože u NodeCopy je délka hrany často 1, údaj o délce se v tomto
případě vynechává; pokud je délka hrany
větší než jedna: 0 znamená, že řetězec končí přímo v uvedeném uzlu, 1 odpovídá pozici o 1
znak dolů z otce uzlu atd.
Oba výše zmíněné údaje jsou zapsány (každý zvlášť) obyčejným binárním kódem s
fázováním (viz A2, 3. vylepšení); kolik bitů mám pro binární kód použít,
snadno zjistím z celkového počtu vnitřních vrcholů či z délky celé použité hrany (oba
tyto údaje jsou známy dekompresoru, takže ví kolikabitová čísla má číst).
Kódová slova pro LeafCopy jsou zapisována pomocí start-step-stop kódů.
Po bitovém příznaku následuje délka nejdelší shody na hraně od otce
dolů do listu zapsaná (1, 1, 11) kódem, protože tato délka nemůže být 0,
kód 0 znamená, že bude následovat řetězec literálů (za 0 tedy následuje
jako u A2 (0, 1, 5) kód délky řetězce a pak posloupnost ASCII kódů). Kód
(1, 1, 11) dovoluje zapsat délku shody až 4094 znaků.
Opět se zde používá trik známý již z metody A2: Protože po řetězci literálů kratším
než maximální délka (63) nemůže následovat další řetězec literálů, následuje-li
LeafCopy, délku shody posuneme o 1 dolů (tedy délka shody 1 bude zapsána jako 0 atd.).
Po délce shody následuje číslo příslušného listu (což jednoznačně odpovídá
zapsání pozice (způsobem jako u metody B2) v prohlížecím okně, na které řetězec
odpovídající listu začíná) zapsané (10,2,14) kódem, resp. jeho vylepšením
uvedeným u metody A2 (kód (10 - x, 2, 14 - x) +
fázování).
Dekompresor pro metodu C2
Narozdíl od metod A2 a B2, dekompresor pro metodu C2 si musí udržovat stejný
PATRICIA tree jako kompresor mimo jiné proto, aby byl schopen zjistit, kterým pozicím v prohlížecím
okně čísla uzlů odpovídají.
To ovšem není tak obtížné - změníme-li pravidlo pro rozhodování
kompresoru mezi copy tokenem (tedy LeafCopy či NodeCopy) a řetězcem literálů.
Tedy pokud nejdelší shoda je alespoň 2 znaky dlouhá, použijeme vždy kódové
slovo pro LeafCopy či NodeCopy (i pokud jsme doteď zapisovali literal token).
Pro zrychlení budeme opět používat pole "permanentních" uzlů v hloubce 1
(jako u B2).
Zatímco kompresor prochází stromem dolů a tedy v každém uzlu musí nahlédnout do
hašovací tabulky, dekompresor dostává číslo příslušného vrcholu (z něhož zjistí
pozici v prohlížecím okně, ze které má kopírovat) z komprimovaného
souboru a data potřebná k určení délky kopírovaného řetězce. Zkopíruje tedy příslušný
řetězec, posune prohlížecí okno a pak projde stromem nahoru (až ke kořeni) a
aktualizuje všechny ukazatele (v uzlech na této cestě) do prohlížecího okna na
aktuální hodnotu. Protože se strom prochází jen směrem nahoru, hašovací tabulky
dekompresor vůbec nepotřebuje.
S výše uvedeným rozhodovacím pravidlem mezi copy a literal tokeny lze aktualizovat
(přidávat fráze) do slovníku velmi jednoduše - v případě NodeCopy či LeafCopy stačí
připojit nový list k příslušné hraně (vzniká nový vnitřní vrchol) či vnitřnímu
vrcholu a provést výše uvedené projití stromu; v případě literálů stačí připojit nový
list k "permanentnímu" uzlu v hloubce 1 pro každý jeden znak zapsaný jako
literál.
Příklad: Předpokládejme, že obrázek 4 zobrazuje PATRICIA tree pro níže uvedené
prohlížecí okno.
(Není to pravda! Například řetězci začínajícímu na pozici 1 by musel odpovídat
nějaký list (nemohl zde být použit copy token, tedy zde byl použit literál) - ale
takový ve stromě není. Nebudu se snažit vytvořit pro toto okno
korektní PATRICIA tree, protože by byl moc složitý a tím i nepřehledný.)
Zároveň upozorňuji, že na obrázku není použito pole "permanentních" uzlů.
Slovo uzel je zde užíváno ve významu vnitřní vrchol.
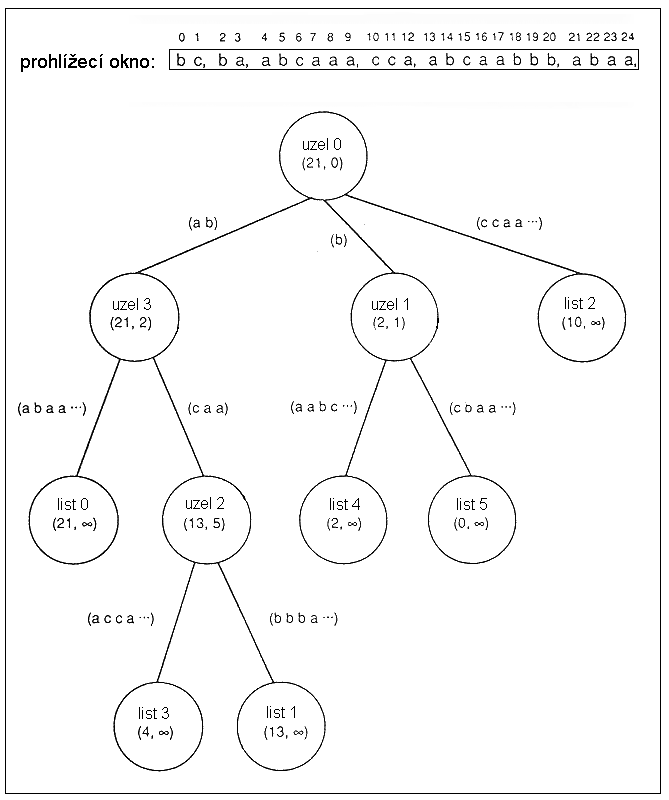
Obrázek 4
Předpokládejme, že následující text k zakódování bude:
- "abcc..."
Pak se použije NodeCopy, protože nejdelší shoda pro tento řetězec ve stromě
je "abc" - tento řetězec končí jeden znak za uzlem 3 na
hraně do uzlu 2. Tedy po bitovém identifikátoru bude zakódována dvojice
(2, 1) příslušnými binárními kódy.
- "abcaaacb..."
Pak bude použito LeafCopy - nejdelší shoda končí na hraně mezi uzlem 2
a listem 3, proto po bitovém identifikátoru bude zapsána (start-step-stop kódy)
dvojice (2, 3).
- "cacbaac..."
Pak bude následovat řetězec literálů - tedy zapíše se flag pro LeafCopy, pak
příslušný (1, 1, 11) start-step-stop kód pro 0, pak
(0, 1, 5) kód délky řetězce (až dokud se nenajde shoda alespoň 2
znaky), tedy zde kód pro 3 a pak následují příslušné znaky - zde
"cac".
Závěr
Algoritmy LZFG dosahují jednoho z nejlepších kompresních poměrů, pokud srovnáváte jen
s klasickými slovníkovými metodami (metodami třídy LZ - ne tedy třeba s
metodou ACB). Jsou to dynamické proudové metody a ve srovnání
s neslovníkovými proudovými metodami (dynamický Huffmanův alg, dynamické aritm.
kódování...), ale i s ACB, jsou velmi rychlé.
Ovšem vhodným spojením statistické metody a slovníkové metody lze dosáhnout lepší
komprese při srovnatelné rychlosti.
Algoritmy LZFG jsou dosti náročné na implementaci, především kvůli složitým datovým
strukturám, a proto se v praxi příliš nepoužívají.
V roce 1990 získali Fiala a Greene patent (4,906,991) na všechny
implementace algoritmu LZ 77 používající stromovou datovou strukturu. Tento patent ovšem pokrývá mnohem větší
množství algoritmů, než Fiala a Greene vymysleli - konkrétně algoritmus Rodeha a Pratta
z roku 1981 (Journal of the ACM, vol 28, no 1, pp 16-24), ale hlavně algoritmy použité
v komprimačních programech lharc, lha a zoo (ještě před pár lety velmi oblíbených).
Použitá literatura:
-
E.R.Fiala, D.H.Greene: Data compression with finite windows. Communications of ACM, 32(4), 490-505, April 1989.
-
T:C.Bell, J.G.Cleary, I.H.Witten: Text Compression. Prentice Hall, Englewood CLiffs, NJ, 1992, odstavec 8.3.12.
-
Salomon D. - Data Compression, Springer, New York 1997, odstavec 3.6.
Zhodnocení literatury
Tento referát byl vytvořen z velké většiny podle článku 1.). Tento
je ovšem napsán tak, že se moc dobře nečte - v některých místech složitá angličtina,
programový kód v nějakém pro mě neznámém jazyku a článek rovněž předpokládá dosti
rozsáhlou znalost problematiky - především ohledně datových struktur (McCreight`s suffix
tree) a operací nad nimi (zmiňuje se o nich okrajově a lze z něj pochopit (obtížně!!) jen
úplné základy - ne například linearitu přidávání do suffix tree apod.). Rovněž obrázky
datových struktur by si zasloužily rozsáhlejší komentář.
Obrázky 1 - 3 původně pocházejí z tohoto článku (ale některé byly samozřejmě upraveny).
V době vytváření tohoto článku, byl ovšem 1.) jediným "slušným" zdrojem
informací.
Zbylé 2 knihy tomuto tématu věnují jen málo prostoru (jsou to obecné knihy o
kompresi) - popisují jen vybrané metody třídy LZFG a to ještě málo podrobně.
Konkrétně 2.) se zabývá jen metodou C2 (o ostatních se ani nedozvíte, že existují)
a je z ní převzat (po upravení) obrázek 4 (původně Figure 8-14). Který je sice použitelný
jako příklad(nechtělo se mi kreslit korektní, dalo by to moc práce), ale je
chybný !!! - není to PATRICIA tree příslušný k uvedenému textu
(proč viz výše), což si autor vůbec neuvědomil!!!
Kniha 3.) se pro změnu zabývá jen metodami A1 a A2, zbytečně rozebírá triviality,
ale vůbec se nezmiňuje o vhodných datových strukturách a proto pro člověka, který zná
metodu LZ 77 a start-step-stop kódy, přináší jen velmi málo nového. Naopak je nepřesná
ohledně toho, kdy u metody A2 (3. vylepšení) použít fázování (i při začátku komprese při
obvyklé velikosti okna - dokud se zcela nezaplní) a obsahuje zásadní chybu ohledně
způsobu jak fázování funguje - konkrétně u příkladu s 16K oknem a 11264 potřebnými
hodnotami uvádí špatná čísla ohledně počtu kódů tvaru "11" následováno 13 bitovým číslem
a "11" následováno 14 bitovým číslem. Tato chyba je ovšem velmi významná, pokud se budete
snažit fázování dle článku 3.) pochopit!!! Korektní hodnoty lze nalézt výše.
Zde si můžete stáhnout celý program pro vizuální předvedení, jak
fungují start-step-stop kódy. Program je napsán v programovacím jazyce C a lze
ho zkompilovat třeba pomocí Borland C++ 3.1 for DOS. Program má za úkol jen předvést,
jak kódování funguje, tedy není "blbuvzdorný".
Tento článek smí být používán libovolně, za předpokladu, že nebude modifikován a že takto
bude učiněno se zmínkou o autorovi a odkazem na stránku
http://jt.sf.cz, odkud by měla být dostupná aktuální verse tohoto
článku.
Snažím se, aby informace zde uvedené byly pravdivé a pokud možno přesné, nicméně nenesu žádnou
odpovědnost za to, že tomu tak opravdu je, ani za jakékoli škody, které by někomu v důsledku případných
špatných či nepřesných informací z tohoto článku mohly vzniknout.
Pokud se Vám podaří tento algoritmus implementovat, zkuste mi poslat Váš výtvor - předem děkuji.
Jakékoliv dotazy či připomínky mi můžete poslat mailem.
Zpět na stránku referátů a jiných výtvorů




